---

涡度方程与环流定理

总的来说，大气运动具有明显的涡旋运动特征。例如台风、龙卷、气旋、反气旋

正压大气

• 密度的空间分布只依赖于气压，这种大气状态称为正压大气
• 正压大气中等压面、等密度面、等温面重合在一起
• 静力平衡条件下，正压大气各等压相互平行，因此某一等压面在空间的倾斜状态代表整个等压面的倾斜状态

斜压大气

• 密度的空间分布不仅依赖于气压还依赖于温度。
• 斜压大气中等压面与等温面、等密度面交割的

正压大气是最简单的大气状态，但是大气本身受热不均匀，以及大气本身的运动，都会破坏大气的原有正压状态。

大尺度大气运动满足静力平衡条件，依据静力平衡概念，容易说明斜压大气中地转风必然要随高度改变。地转风大小与等压面坡度成正比，若等压面坡度随高度改变，则地转风必随高度改变。等压面坡度随高度改变是由于等压面上温度分布均匀即大气斜压性所致。

• 正压大气中等压面坡度不随高度改变，地转风也就不随高度改变。
• 斜压大气是地转风随高度改变的充分与必要条件
• 正压大气是地转风不随高度改变的充分与必要条件

用p坐标系中的地转风表达式容易导出地转风随高度变化的方程。p坐标系中地转风表达式为：

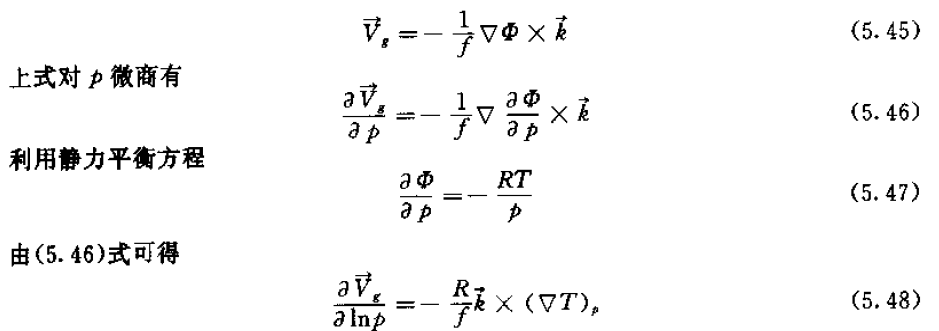
上述方程为热成风方程，实际上它是地转风铅直切变与等压面上水平温度直接的关系式。若大气是正压的，等压面与等温面重合，故地转风不随高度变化。

热成风定义：

• 铅直方向上两等压面上地转风的矢量差
• 两等压面之间的厚度与平均温度成正比

• 热成风方向与等平均温度线平行，在北半球，暖区在热成风方向右侧，冷区在左侧
• 热成风大小与平均温度梯度成正比，与纬度的正弦成反比
• 地转风向随高度逆时针转动，与此相伴随的有冷平流；随高度顺时针转动，与此相伴随的暖平流

地转风的关系的重要性揭示了大尺度运动中风场和水平气压场之间的基本关系，热成风关系的重要性在于具体地揭示了静力平衡大尺度运动中风场、气压场、温度场之间的关系

绝对环流定理

速度环流：

• 流场中有某一闭合物质曲线上的速度切向分量沿该闭合物质曲线的线积分，定义为速度环流，简称为环流。以C代表环流，

由于下垫面受到非均匀加热，由于静力平衡方程，等比压面要向冷区倾斜，高温处比容大，低温处比容小，等比容面向暖区倾斜，使得大气由正压转变为斜压。

铅直环流型式是由于非均匀加热造成的，所以称为直接热力环流，通常解释海陆风和山谷风的形成。

正压大气中绝对环流守恒，也就是开尔文环流定理。

• 大气的斜压性归结为非均匀加热的结果，正压大气的等压面和等比容面彼此与地面平行。

相对环流定理

对于气象问题来说， 考虑空气微团相对于地球的运动，才具有实际意义

对于绝对速度进行积分，得到相对环流和牵连环流： \(C_a=C+C_e\) 牵连环流：由于地球旋转作用引起的

假设运动是水平的，初始环流取在水平面上，如下图所示：

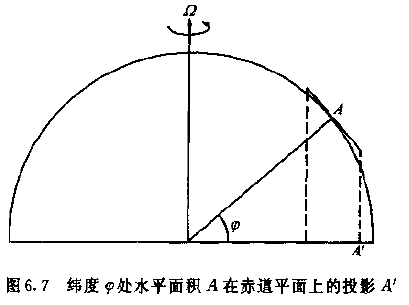\(A'=A\sin\overline\psi\)

1. 环线所包围的面积改变和平均纬度改变都可引起相对环流发生变化

2. 环线包围的面积改变与水平辐合辐射有关

3. 纬度的改变与流体的南北向运动有关

---

涡度

数学上定义为：

• 速度场的旋度，是流体旋转运动的量度
• 散度也是由速度场决定的物理量，反应的是流体膨胀运动的量度。

描述为流体微团旋转快慢的物理量，是一个微观描述

如下所示 \(\overline\omega\) 相对涡度由两个部分组成：切变涡度和曲率涡度

切变涡度：河流中心流速较大，树叶会随着河水向下游运动且打转==》切变的平直流动中存在涡旋

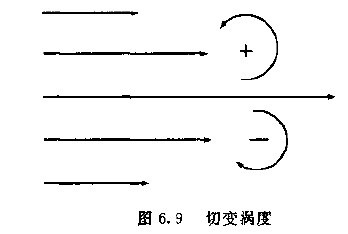
曲率涡度: 发现河流方向发生急剧改变的地方，容易观测到涡旋

流函数和速度势

无辐散运动，即纯粹的涡旋运动，其运动条件为：

$\delta=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$

无旋运动是大气的另一种基本形式，其满足条件为：

$\xi=\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}=0$

铅直涡度方程

对于天气尺度运动，可以从简化的水平动量方程导出涡度方程，z坐标下的水平动量方程为：

\[\begin{aligned}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial x}-fv&=-\frac1\rho\frac{\partial p}{\partial x}\\\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}+fu&=-\frac1\rho\frac{\partial p}{\partial y}\end{aligned}\]

第二行对x求导，第一行对y求导，然后将所得结果相减，注意到:

$\xi=\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}=0$

便得到涡度方程

\[\begin{aligned}\frac{\partial\xi}{\partial t}+u\frac{\partial\xi}{\partial x}+v\frac{\partial\xi}{\partial y}+w\frac{\partial\xi}{\partial z}+(\zeta+f)\left|\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right|\\+\left|\frac{\partial w}{\partial x}\frac{\partial v}{\partial x}-\frac{\partial w}{\partial y}\frac{\partial u}{\partial x}\right|+v\frac{\mathrm{d}f}{\mathrm{d}y}&=\frac1{\rho^2}\Big(\frac{\partial\rho}{\partial x}\frac{\partial\rho}{\partial y}-\frac{\partial\rho}{\partial y}\frac{\partial\rho}{\partial x}\Big|\end{aligned}\]

地转参数$f$ 仅依赖于$y$, 得$\frac{df}{dt} = v\frac{df}{dy}$ .于是涡度方程可以写为：

\[\frac{\mathrm{d}(\xi+f)}{\mathrm{d}t}=-(\zeta+f)\left|\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right|-\left|\frac{\partial w}{\partial x}\frac{\partial v}{\partial x}-\frac{\partial w}{\partial y}\frac{\partial u}{\partial x}\right|+\frac1{p^2}\left|\frac{\partial\rho}{\partial x}\frac{\partial\rho}{\partial y}-\frac{\partial\rho}{\partial y}\frac{\partial\rho}{\partial x}\right|\]

其中，$\xi + f \equiv \xi_a$ 为绝对涡度的铅直分量。上式表明空气微团绝对涡度随时间的变化率由右端三项决定，分布是：散度项、涡管扭曲项、力管项

散度项

$\left[\frac{\mathrm{d}(\zeta+f)}{\mathrm{d}t}\right]_1=-\left.(\zeta+f)\right

\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}$

中高纬 $\xi$ 大于为 $10^{-5}$/s , 而 $f$ 大于为 $10^{-4}$/s ,所以一般情形下 $(\zeta+f)$为正值。

因此，当有水平辐散时，绝对涡度要减小；当有水平辐合时，绝对涡度要增加

固体转动时，无外力矩作用下角动量守恒，转动惯量发生改变会引起角速度的变化。水平散度引起绝对涡度变化的机制与上述情形是类似的。正压流体中绝对涡度强度守恒，当有水平辐合辐散时，将引起涡管的水平截面积改变，从而引起绝对涡度的变化。

水平辐散 辐合引起的涡度变化的机制，对于 天气尺度扰动的发展是非常重要的。

一般情况下， \(\zeta+f\) 大于零，因此，当有水平辐射时，绝对涡度要减小；有水平辐合时，绝对涡度要增加。

涡度扭曲项

\[\left[\frac{\mathrm{d}(\zeta+f)}{\mathrm{d}t}\right]_2=-\left(\frac{\partial w}{\partial x}\frac{\partial v}{\partial x}-\frac{\partial w}{\partial y}\frac{\partial u}{\partial z}\right)\]

可以改写为

\[\begin{aligned}-\left|\frac{\partial w}{\partial x}\frac{\partial v}{\partial z}-\frac{\partial w}{\partial y}\frac{\partial u}{\partial x}\right|&=\xi\frac{\partial w}{\partial x}+\eta\frac{\partial w}{\partial y}\\\\\end{aligned}\]

其中：

\[\eta\equiv\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x}\] \[\xi\equiv\frac{\partial w}{\partial y}-\frac{\partial v}{\partial z}\]

$\xi 和 \eta$ 分别是涡度矢量在x和y方向的分量，也是他们的水平涡度

\[\left[\frac{\mathrm{d}(\zeta+f)}{\mathrm{d}t}\right]_2=\xi\frac{\partial w}{\partial x}+\eta\frac{\partial w}{\partial y}\]

上式表明，当有水平涡度存在时，如果铅直速度水平不均匀，就会引起涡度铅直分量的变化。

从物理上看，这项表示涡管位移扭曲，使得涡管相对水平面的倾斜度发生改变引起的涡度铅直分量的变化。

力管项

\[\left[\frac{\mathrm{d}(\xi+f)}{\mathrm{d}t}\right]_3=-\frac1{\rho^2}\left[\frac{\partial\rho}{\partial x}\frac{\partial\rho}{\partial y}-\frac{\partial\rho}{\partial y}\frac{\partial\rho}{\partial x}\right]\]

这一项代表大气的斜压性对绝对涡度的作用

涡度方程的尺度分析

各特征尺度如下：

水平尺度

铅直尺度

水平速度尺度

垂直速度尺度

时间尺度

地转参数

beta参数

重力加速度

\[\begin{aligned} &L\sim10^{6}\mathrm{m} \\ &D\sim H\sim10^{4}\mathbf{m} \\ &U\sim10^{1}\mathbf{m}/\mathbf{s} \\ &\mathbf{W}\sim10^{-2}\mathbf{m}/\mathbf{s} \\ &\tau\sim\frac{L}{\bar{U}}\sim10^{5}\mathbf{s} \\ &f_{\mathfrak{o}}\sim10^{-4}/\mathbf{s} \\ &{\frac{\mathrm{d}f}{\mathrm{d}y}}={\frac{2\boldsymbol{\Omega}\mathrm{cos}\varphi}{a}}\sim10^{-11}\mathbf{m}/\mathbf{s} \\ &\mathbf{g}\sim10\mathbf{m}/\mathbf{s}^{2} \end{aligned}\]

此外还有，

\[\begin{aligned} &\delta\equiv\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\sim\frac{W}{H}\sim10^{-6}/s \\ &\frac{1}{\rho}\frac{\partial p}{\partial x}\sim\frac{1}{\rho}\frac{\partial p}{\partial y}\sim f_{\phi}U\sim10^{-3}\mathrm{m/s^{2}} \\ &\frac{\partial\ln\rho}{\partial x}\sim\frac{\partial\ln\rho}{\partial y}\sim\frac{f_{0}U}{gH}\sim10^{-8}/\mathfrak{m} \end{aligned}\] \[\begin{aligned}&\xi\sim\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\sim\frac UL\sim10^{-5}/\mathbf{s}\\&\frac\xi\delta\sim\frac UL\frac H{\bar{W}}\sim10^{\circ}\end{aligned}\]

对于天气尺度运动系统，相对涡度比水平散度大一个量级，又

\[\frac\zeta f\sim\frac U{f_0\overline{L}}\equiv Ro\sim10^{-1}\]

所以相对涡度比牵连涡度小一个量级，所以涡度方程散度项中的$\xi$ 相对于f可以忽略不计，即

\[(\xi+f)\left|\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}\right|\simeq f\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)\] \[\begin{aligned} &\frac{\partial\boldsymbol{\zeta}}{\partial\boldsymbol{t}}\sim\frac{U^2}{L^2}\sim10^{-10}/\mathbf{s}^2 \\ &u\frac{\partial\boldsymbol{\zeta}}{\partial x}\sim\frac{U^2}{L^2}\sim10^{-10}/\mathbf{s}^2 \\ &v\frac{\partial\boldsymbol{\zeta}}{\partial\boldsymbol{y}}\sim\frac{U^2}{L^2}\sim10^{-10}/\mathbf{s}^2 \\ &w\frac{\partial\xi}{\partial z}\sim\frac{Uw}{LH}\sim10^{11}/s^{2} \\ &\beta v\sim U\beta\sim10^{-10}/s^{2} \\ &f\Big|\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\Big|\sim\frac{f_0W}H\sim10^{-10}/s^2 \\ &\left|{\frac{\partial\boldsymbol{w}}{\partial x}}{\frac{\partial\boldsymbol{v}}{\partial\boldsymbol{z}}}-{\frac{\partial\boldsymbol{w}}{\partial y}}{\frac{\partial\boldsymbol{u}}{\partial\boldsymbol{z}}}\right|\sim{\frac{\boldsymbol{W}\boldsymbol{U}}{\boldsymbol{H}\boldsymbol{L}}}\sim10^{-\mathbf{u}ı}/\mathbf{s}^{2} \\ &\frac1{\rho^2}\left|\frac{\partial\rho}{\partial x}\frac{\partial\rho}{\partial y}-\frac{\partial\rho}{\partial y}\frac{\partial\rho}{\partial x}\right|\sim\frac{f_0^2U^2}{gH}\sim10^{-11}/s^2 \end{aligned}\]

保留涡度方程中的量级大项，得到适用于天气尺度运动的近似涡度方程：

\[\begin{aligned}\frac{\partial\boldsymbol{\xi}}{\partial t}+u\frac{\partial\boldsymbol{\xi}}{\partial\boldsymbol{x}}+v\frac{\partial\boldsymbol{\xi}}{\partial\boldsymbol{y}}+\beta\boldsymbol{\upsilon}&=-f\Bigl(\frac{\partial\boldsymbol{u}}{\partial x}+\frac{\partial\boldsymbol{v}}{\partial\boldsymbol{y}}\Bigr)\\\\\frac{d_k(\boldsymbol{\xi}+f)}{\mathrm{d}t}&=-f\Bigl(\frac{\partial\boldsymbol{u}}{\partial x}+\frac{\partial\boldsymbol{v}}{\partial y}\Bigr)\\\\\frac{\mathrm{d}_k}{\mathrm{d}t}&\equiv\frac\partial{\partial t}+u\frac\partial{\partial\boldsymbol{x}}+v\frac\partial{\partial\boldsymbol{y}}\end{aligned}\]

上式表明，在天气尺度水平运动中，微团的绝对涡度的变化，完全是散度作用的结果。

如果进一步认为运动是水平无辐散的，则绝对涡度是守恒的:

\[\frac{\mathrm{d}_A(\xi+f)}{\mathrm{d}t}=0\]

• 上式也称为正压涡度方程。

涡度方程和散度方程-等压坐标系

p坐标系又被成为等压的坐标系，不考虑摩擦的情况下，p坐标系的水平运动方程为：

\[\begin{cases}\left(\frac{\partial u}{\partial t}\right|_p+u\Big(\frac{\partial u}{\partial x}\Big|_p+v\Big|\frac{\partial u}{\partial y}\Big|_p+w\frac{\partial u}{\partial p}=-\left|\frac{\partial\Phi}{\partial x}\right|_p+fv\\\left|\frac{\partial v}{\partial t}\right|_p+u\Big|\left.\frac{\partial v}{\partial x}\right|_p+v\Big|\left.\frac{\partial v}{\partial y}\right|_p+w\frac{\partial u}{\partial p}=-\left|\frac{\partial\Phi}{\partial y}\right|_p-fu\end{cases}\]

局地变化项+散度项=压力项+科氏力项

对上述两式分布对x和y方向求导再相减，得到：

\[\begin{aligned} \frac{\partial\boldsymbol{\zeta}_{\boldsymbol{\rho}}}{\partial\boldsymbol{t}}=& -u\left(\frac{\partial\xi_p}{\partial x}\right|_p-v\left(\frac{\partial\xi_p}{\partial y}\right|_p-w\frac{\partial\xi_p}{\partial p}-(\zeta_p+f)\left[\left(\frac{\partial u}{\partial x}\right|_p+\left(\frac{\partial v}{\partial y}\right|_p\right]_p \\ &-v\Big[\left.\frac{\partial f}{\partial y}\right|_p+\left[\left(\frac{\partial w}{\partial y}\right)_p\frac{\partial u}{\partial p}-\left(\frac{\partial w}{\partial x}\right)_p\frac{\partial v}{\partial p}\right] \end{aligned}\]

右端

• 第一、第二项为相对涡度平流项
• 第三项为相对涡度的铅直输送项
• 第四为散度项
• 第五为β项
• 第六为扭曲项

与p坐标系涡度方程中少了一个力管项，实际上，大气斜压效应将反映在散度项中。

• 大气的斜压性是等压面上水平散度不为零的必要条件，亦即只要是大气是斜压的，p坐标涡度中的散度项可能对涡度的变化有作用，故大气的斜压效应是间接地通过散度项起作用的。

散度方程

涡度的局地变化是与水平散度紧密相联系的，在研究涡度及其随时间变化的同时，必须给处水平散度及其变化

\[\begin{aligned} \frac{\partial\delta}{\partial t}=& -u\left(\frac{\partial\delta}{\partial x}\right)_p-v\left(\frac{\partial\delta}{\partial y}\right)_p-w\frac{\partial\delta}{\partial p}-\left(\frac{\partial u}{\partial x}\right)_p^2-\left(\frac{\partial v}{\partial y}\right)_p^2 \\ &-2\left|\frac{\partial u}{\partial y}\right|_p\left|\frac{\partial v}{\partial x}\right|_p-\left[\left|\frac{\partial u}{\partial x}\right|_p\frac{\partial u}{\partial p}+\left|\frac{\partial u}{\partial y}\right|_p\frac{\partial v}{\partial p}\right] \\ &-\left|\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right|_p\Phi+f\zeta_p-u\left|\frac{\partial f}{\partial y}\right|_p \\ &\delta=\left\langle\frac{\partial u}{\partial x}\right\rangle_{p}+\left\langle\frac{\partial v}{\partial y}\right\rangle_{p} \end{aligned}\]

为等压面上水平散度，令：

\[\begin{aligned} \vec{\boldsymbol{v}}=& ui+vj \\ \nabla_{p}=& \vec{i}\left(\frac\partial{\partial x}\right)_p+\vec{j}\left(\frac\partial{\partial y}\right)_p \\ \nabla_{p}^{2}=& \left|\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}\right|_{p} \\ J_{\rho}(u,v)=& \left|\left.\frac{\partial u}{\partial x}\right|_{p}\left|\frac{\partial v}{\partial y}\right|_{p}-\left|\frac{\partial v}{\partial x}\right|_{p}\left|\frac{\partial u}{\partial y}\right|_{p}\right. \end{aligned}\]

则上式可改写为：

\[\begin{aligned} \frac{\partial\delta}{\partial t}=& -\bar{V}\cdot\nabla_p\delta-\omega\frac{\partial\delta}{\partial p}-\nabla_p^2\Phi-\nabla_p\omega\cdot\frac{\partial\vec{V}}{\partial p}-\delta^2+2J_p(u,v) \\ &+f\xi_p-(\vec{k}\times\vec{V})\cdot\nabla_pf \end{aligned}\]

方程左端为：水平散度的局地变化

右端为：

• 第一项：散度平流项
• 第二项：散度的铅直输送项
• 第三项：等压面的坡度改变项
• 第四项：水平风俗的铅直切变效应
  • 当有风的铅直切变时，等压面上铅直速度分布的不均匀将引起散度的变化
• 第五项：散度平方项
  • 无论是对于水平辐散的气流，还是辐合的气流，引起辐合的加强或辐散的减弱
• 第六项：形变项
  • 表示风场的水平切变对散度变化的作用

位势涡度守恒定律

海洋中的位涡表达式是总涡度除以水深。位涡守恒的实质是角动量守恒。引起位涡变化的只有外力和斜压，内部作用可以改变涡度但不能改变位涡。

所以，位涡方程就是考虑涡度变化的几个因素：内部作用、斜压项、外力项

内部作用包括：

• 水平流速垂直剪切引起的涡管倾斜和辐合辐散

位涡：

• 综合动力作用和热力作用的物理量

位涡方程由涡度方程、连续方程、位温方程导出，位涡守恒的条件为：绝热无摩擦

考虑一个流体单元，当斜压背景下存在一个扰动，斜压效应会引起流体单元发生旋转，原本存在的背景涡度f，由于斜压的作用，引起水平方向上涡度的增加，涡管发生倾斜，总涡度增加，造成水平速度的垂直剪切。

位涡守恒定律

假设大气作干绝热运动，这时空气微团位温守恒，等位温面为一物质面，空气微团沿等位温面运动。在两相邻的等位温面之间取一个和等位温面相垂直的小住体

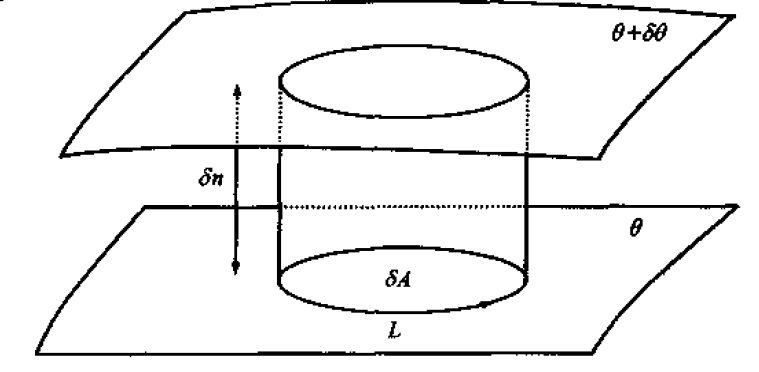
前提条件：

• 上述小柱体在运动中虽然可以伸长缩短，但其包含的治理不随时间变化
• 利用位温的定义，利用状态方程
• 将无摩擦的绝对环流定理用于等位温面上

\[\begin{aligned}q&=\frac{(\nabla_3\times\vec{V}_a)\bullet\nabla_a\theta}\rho=\text{常数}\\\\\frac{\mathrm{d}q}{\mathrm{d}t}&=\frac{\mathrm{d}}{\mathrm{d}t}\Big[\frac{(\bigtriangledown_3\times\vec{V}_a)\bullet\bigtriangledown_a\theta}\rho\Big]=0\end{aligned}\]

上式定义为：位势涡度，简称为位涡，上式表明：

• 在无摩擦干绝热运动中微团的绝对涡度虽然可以变换，但是位涡却是守恒的，这就是埃特尔位涡守恒定律。

位涡守恒方程的简化

为了适用于应用，使用尺度分析方法对位涡方程进行简化，

\[\begin{cases}\xi_a=\xi=\left(\frac{\partial w}{\partial y}-\frac{\partial v}{\partial z}\right)\\\eta_a=\eta+\widetilde{f}=\left(\frac{\partial u}{\partial x}-\frac{\partial w}{\partial x}\right)+2\Omega\mathrm{cos}\varphi\\\xi_a=\xi+f=\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)+2\Omega\mathrm{cos}\varphi\end{cases}\]

各项量级如下：

\[\begin{aligned} &&&\frac{a\ln\theta}{\partial x} \sim\frac{\partial\ln\theta}{\partial y}\sim\frac{f_{o}U}{gH}\sim10^{-s}/\mathrm{m} \\ &&&\frac{\partial\ln\theta}{\partial z} \sim\frac1{10\overline{H}}\sim10^{-5}/\mathfrak{m} \\ &&&\xi_{a}=\frac{\partial w}{\partial y}-\frac{\partial v}{\partial z}\sim\frac{W}{L}-\frac{U}{H}\sim10^{-3}/\mathbf{s} \\ &&& \eta_a=\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x}+2\Omega\mathrm{cos}\varphi\sim\frac UH-\frac WL+\widetilde{f}_0\thicksim10^{-3}/\mathrm{s} \\ &&&\zeta=\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}+2\Omega\mathrm{sin}\varphi\sim\frac{U}{L}+f_{0}\sim10^{-4}/\mathrm{s} \\ &&&\xi_{a}{\frac{a\mathbf{ln}\theta}{\partial x}}\sim10^{-11}/({\mathfrak{m}}\cdot{\mathfrak{s}}) \\ &&&\eta_{a}\frac{\partial\mathbf{ln}\theta}{\partial\mathbf{y}}\sim10^{-11}/(\mathbf{m}\cdot\mathbf{s}) \\ &&&\zeta_{a}\frac{\partial\ln\theta}{\partial z}\sim10^{-8}/({\mathfrak{m}}\cdot{\mathfrak{s}}) \end{aligned}\]

使用尺度分析，略去小项，简化得到：

\[\frac{(\triangledown_3\times\vec{V}_x)\cdot\triangledown_3\theta}\rho\simeq\frac1\rho(\zeta+f)\frac{\partial\theta}{\partial z}\]

写成：

\[\frac{\mathrm{d}}{\mathrm{d}t}[\frac1\rho(\xi+f)\frac{\partial\theta}{\partial z}]=0\]

由位涡的定义来看，位涡是一个标量，是一个综合表征大气运动状态和热力状态的物理量，它的主要性在于干绝热无摩擦运动中微团的位涡是守恒的。位涡守恒定律揭示了涡度变化是受到大气热力结构制约的。在静力平衡条件下，简化的位涡形式为：

\[\frac1\rho\triangledown_3\vec{V}_a\cdot\nabla_3\theta\approx\frac1\rho\left(\xi+f\right)\frac{\partial\theta}{\partial z}=-\left(\xi+f\right)\frac{\partial\theta}{\partial p}\approx\frac{\left(\xi+f\right)\partial\theta}{\partial p}\]

在绝热过程中，两个位温面之间的位温差不变，

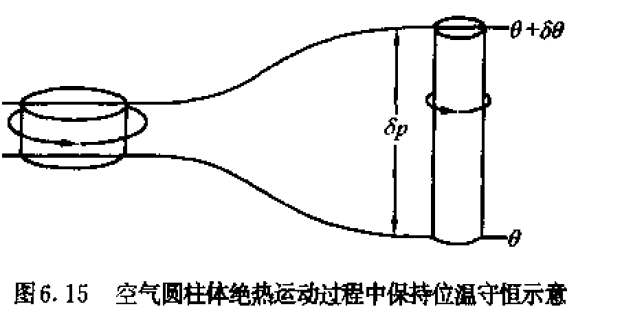
位涡在某种意义下是涡旋强度与其有效厚度之比的一个度量，根据位涡守恒原则， 有效厚度增加，则绝对涡度增大。

---

吕美仲, 侯志明, 周毅. 动力气象学[M]. 气象出版社, 2004.